Urutan Bilangan Bulat – Pq (dibaca p lebih dari q) maka dan hanya q<p, atau ada bilangan bulat positif s sehingga q + s = p.
3 Contoh: – 5 < -2, karena ada bilangan bulat positif 3, maka (-5) + 3 = (-2) -3 < 7, karena ada bilangan bulat positif 10, maka (-3) + 10 = 7.
Urutan Bilangan Bulat
Jika p dan q bilangan bulat, maka salah satu dari tiga kemungkinan benar: p q
Soal & Kunci Jawaban Matematika Kelas 6 Halaman 56 57 58: Urutan Bilangan Bulat, Hitung Suhu Ruangan
5 Teorema ini berlaku untuk bilangan bulat a, b, c, jika a = b, maka a + c = b + c, jika a<b, maka a + c <b + c
6 Teorema bilangan bulat a, b, dan c Jika a = b, maka ac = bc Jika a 0, maka ac < bc Jika a < b dan c bc
Teorema 7 (Sifat transitif barisan bilangan bulat) untuk bilangan bulat a, b, dan c Jika a < b dan b < c, maka a < c.
Untuk mengoperasikan situs web, kami mendaftarkan data pengguna dan menyediakannya untuk entitas pemrosesan. Untuk menggunakan situs web ini, Anda harus menerima kebijakan privasi kami, termasuk kebijakan cookie kami. Bilangan adalah satuan matematika terkecil yang didefinisikan dengan cara tertentu. Bilangan adalah sekumpulan bilangan tertentu yang terdefinisi. Contoh angka: 1 (default “satu”), – 8 (default “delapan”) dst. Contoh dengan angka: 1, 2, 3, 4, … dst. (default “bilangan asli”)
Kunci Jawaban Matematika Kelas 2 Halaman 31 34 Kurikulum Merdeka, Lengkapi Urutan Bilangan Berikut!
Garis bilangan digunakan untuk menjumlahkan bilangan bulat. Jika suatu bilangan dijumlahkan dengan bilangan bulat positif, tanda panahnya akan mengarah ke kanan, dan jika bilangan tersebut dijumlahkan dengan bilangan bulat negatif, maka panahnya akan menunjuk ke kiri. Semakin tinggi angka di sebelah kanan, semakin rendah angka di sebelah kiri. Garis bilangan ini untuk tampilan horizontal, disebut juga tampilan lanskap.
5 Garis Bilangan Cobalah untuk mengisi titik-titik pada garis bilangan berikut dengan angka yang benar. Jawaban: 4 5 6 7 8 9 10 11
Pada. Membaca Bilangan Bulat Himpunan bilangan bulat yang terdiri dari bilangan bulat positif, bilangan bulat negatif dan nol, yaitu : netral Bilangan bulat negatif Bilangan bulat positif
Deskripsi dan contoh Garis bilangan atas mewakili himpunan bilangan bulat. Panah kanan menunjukkan bilangan positif (bilangan bulat positif di sebelah kanan nol). • Panah kiri menunjukkan bilangan negatif (bilangan bulat negatif berada di sebelah kiri nol). • Perhatikan garis bilangan! Kapan nilainya akan lebih tinggi dan kapan lebih rendah? Ternyata semakin ke kanan suatu bilangan pada garis bilangan, maka semakin besar pula bilangan tersebut. Sebaliknya, semakin ke kiri suatu bilangan pada garis bilangan, maka semakin rendah nilai bilangan tersebut. Contoh: bilangan Simbol bilangan berbunyi 1 satu 2 3 tiga -2 negatif dua 4 -4 negatif empat
Urutan Bilangan Bulat Dari Terkecil Dibawah Ini Yang Benar Adalah Di Kasih Cara Kerja Yaa Kak
Mengurutkan bilangan dari terkecil ke terbesar dan sebaliknya Mengurutkan bilangan bulat dari terkecil ke terbesar Mengurutkan bilangan : 1, 6, 0, 5, 4, 2, 7, – 1, – 2, -3, 3 Perhatikanlah barisan bilangan berikut , Anda dapat melihat urutan dari yang terkecil: -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7
11 Mengurutkan bilangan bulat Mengurutkan bilangan bulat dari terkecil ke terbesar Silakan pilih urutan yang benar pada pertanyaan di bawah ini. Buku Kerja, hal.13 3 Latihan 1.2 Mengurutkan bilangan: -8, -3, -5, -1, 0, 1, -4, -7, -6, 2, -2 2, -1, 4, 0, 7, -2, 3, 1, 5, -3, 6 -3, 0, 4, 2, -2, 3, 1, -1, 5, -4 -8, -7, -6, -5, -4, – 3, -2, -1, 0, 1, 2 -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7 -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
Mengurutkan bilangan bulat dari terbesar ke terkecil Mengurutkan bilangan bulat dari terbesar ke terkecil hampir sama dengan mengurutkan dari terkecil ke terbesar, hanya saja urutannya dibalik Mengurutkan bilangan : 1, 6, 0, 5, 4, 2, 7, – 1 , – 2 , -3, 3 Perhatikan barisan bilangan berikut: terlihat barisan bilangan terbesar adalah 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3
13 Mengurutkan Bilangan Bulat Mengurutkan bilangan bulat dari yang terbesar ke terkecil Pada soal-soal di bawah ini, pilihlah urutan yang benar. Buku Kerja, hal.13 3 Latihan 1.2 Mengurutkan bilangan: -8, -3, -5, -1, 0, 1, -4, -7, -6, 2, -2 2, -1, 4, 0, 7, -2 , 3, 1, 5, -3, 6 -3, 0, 4, 2, -2, 3, 1, -1, 5, -4 2, 1, 0, -1, -2, -3, – 4, -5, -6, -7, -8 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3 5, 4, 3, 2, 1 , 0, – 1, -2, -3, -4
Tip Trik Mengurutkan Bilangan Pecahan Bulat Dan Bilangan Pecahan Campuran
2 2 (3 lebih dari 2) -2> -3 (-2 lebih kecil dari -3) dapat ditulis juga -3<-2 (-3 kurang dari – 2) Kedua bentuk ini mempunyai pengertian yang sama, hanya bentuknya saja yang berbeda. Mari kita berlatih: Tentukan urutan bilangan berikut yang benar! 0 ………………… -9 -7 ……………….. 12
Untuk mengurangkan bilangan bulat, terlebih dahulu konversikan bilangan tersebut ke bentuk penjumlahan. 1) Mengurangi bilangan bulat positif dari bilangan bulat positif. adalah –14 2 ) Mengurangkan bilangan bulat positif dari bilangan bulat negatif 21 – (–7) = 21 + (–7 berlawanan) = = 28
3) Mengurangkan bilangan bulat negatif dari bilangan bulat positif Contoh: –32 –13 = –32 + (melawan 13) = –32 + (–13) = –45 4) Mengurangkan bilangan bulat negatif dari bilangan bulat negatif –11 – ( – 9) = –11 + (melawan -9) = –11 + 9 = –2
Pada. Mengalikan bilangan bulat 1) Mengalikan bilangan bulat positif dengan bilangan bulat positif Contoh: a) 8×5 = 5×8 = 40 b) 3×5×9 maka didapat 3×5×9 = 15×9 = 135 atau 3 × 5 × 9 = 3 × 45 = 135 2) Perkalian bilangan bulat positif dengan bilangan bulat negatif a) 6 × (–3) = –3 + (–3) + (–3) + (–3) + (– 3) ) + ( –3) = –18 b) –11 × 5 = 5 × (–11) (dengan adanya sifat komutatif) = (–11) + (–11) + (–11) + ( – 11 ) + ( – 11) = -55
Soal & Kunci Jawaban Matematika Kelas 6 Sd Halaman 56 57 58 Kurikulum Merdeka: Urutan Bilangan Bulat
3) Mengalikan bilangan bulat negatif dengan bilangan bulat negatif Contoh: a) –2 × (–3) = …. b) –7 × (–2)= ….. Bagaimana menjawabnya? Lihat rumus perkalian di bawah ini! a) –2 × 3 = –6 +2 –2 × 2 = –4 –2 × 1 = –2 –2 × 0 = 0 –2 × (–1) = 2 –2 × (–2) = 4 – 2 × (–3) = 6 b) Dengan menggunakan cara yang sama seperti a, kita peroleh: –7 × (–2) = 14 Oleh karena itu –7 × (–2) = 14 Catatan: Bilangan positif dikalikan bilangan negatif menghasilkan hasilnya angka negatif. Bilangan negatif dikalikan dengan bilangan negatif menghasilkan bilangan positif.
Contoh: 1) 36 : 4 = 9 karena 4 × 9 = 36 2) 72 : –9 = –8 karena –9 × (–8) = 72 3) –98 : 7 = –14 karena 7 × ( –14) = –98 4) –156 : (–12) = 13 karena (–12) × 13 = –156 Bila bilangan bulat dibagi, didapat: • Bila bilangan positif dibagi dengan bilangan positif, didapat bilangan positif • Bilangan positif dibagi bilangan negatif menghasilkan bilangan negatif • Bilangan negatif dibagi bilangan positif menghasilkan bilangan negatif • Bilangan negatif dibagi bilangan negatif menghasilkan bilangan positif
1) Sifat komutatif penjumlahan (dapat dilakukan sembarang urutan) Contoh: a) = = 47 b) 58 + (–49) = – = 9 c) – = 47 + (–61) = –14 2) Sifat komutatif perkalian (Anda juga dapat melakukannya dalam urutan apa pun) a) 12 × 4 = 4 × 12 = 48 b) 25 × (–8) = –8 × 25 = –200
1) Gabungan penjumlahan Contoh: 9 + (12 + 8) = (9 + 12) + 8 = 29 = 29 dapat diselesaikan 2) Gabungan perkalian 15 × 6 × 7 dapat diselesaikan 15 × (6) × 7) = ( 15 × 6) × 7 × 15 × 42 = 90 × 7 630 = 630
Diketahui Bilangan Bilangan 0,4, 2, 2, 4. Jika Diurutkan
Contoh: 25 × (40 + 2), maka mudah menghitungnya: 25 × (40 + 2) = (25 × 40) + (25 × 2) = = 1050 g. Menggunakan Sifat Operasi Hitung 1) Penjumlahan = 72 + (8 + 31) = (72 + 8) + 31 = = 80 + ( ) = ( ) + 11 = = 111 b) = ( ) + 35 = = 80 + ( ) = ( ) + 15 = = 115 2) Perkalian a) 35 × 14 = 35 × (2 × 7) = (35 × 2) × 7 = 70 × 7 = 490 b) 20 × 49 = 20 × ( 50 ) – 1 ) = (20 × 50) – (20 × 1) = – 20 = 980
24 6. Pembulatan Bilangan Dalam kehidupan sehari-hari kita sering menaksir suatu besaran. Perkiraan dapat dibuat dengan pembulatan angka. a) Pembulatan
Rumus rumus bilangan bulat, penjumlahan bilangan bulat, bilangan bulat kls 6, pengertian dari bilangan bulat, bilangan bulat terdiri dari, operasi hitungan bilangan bulat, bilangan bulat, perkalian bilangan bulat, contoh penjumlahan bilangan bulat, rumus pembagian bilangan bulat, urutan bilangan, kumpulan soal bilangan bulat

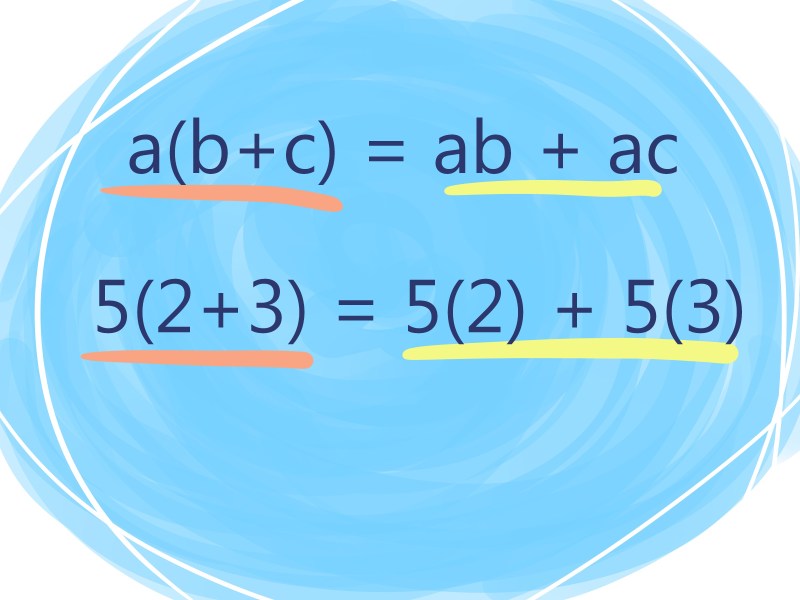



Leave a Comment